4. Focus field (PSF) calculations¶
The free space focus field (PSF) arising from a given back pupil aperture function can be calculated via the Debye diffraction integral. biobeam can evaluate the diffraction integral for a variety of aperture functions directly on the GPU and thus can calculate the 3D PSF (both scalar and vectorial) extremely fast.
4.1. Gaussian/Bessel beams¶
Gaussian/Bessel beams
-
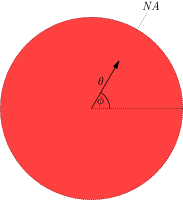
biobeam.focus_field_beam(shape=(128, 128, 128), units=(0.1, 0.1, 0.1), lam=0.5, NA=0.6, n0=1.0, return_all_fields=False, n_integration_steps=200)¶ calculates the focus field for a perfect, aberration free optical system for x polzarized illumination via the vectorial debye diffraction integral (see [1]). The pupil function is given by numerical aperture(s) NA (that can be a list to model bessel beams, see further below)
Parameters: - shape (Nx,Ny,Nz) – the shape of the geometry
- units (dx,dy,dz) – the pixel sizes in microns
- lam (float) – the wavelength of light used in microns
- NA (float/list) – the numerical aperture(s) of the illumination objective that is either a single number (for gaussian beams) or an even length list of NAs (for bessel beams), e.g. NA = [0.5,0.55] lets light through the annulus 0.5<0.55 (making a bessel beam ) or NA = [0.1,0.2,0.5,0.6] lets light through the annulus 0.1<0.2 and 0.5<0.6 making a beating double bessel beam…
- n0 (float) – the refractive index of the medium
- n_integration_steps (int) – number of integration steps to perform
- return_all_fields (boolean) – if True returns also the complex vectorial field components
Returns: - u (ndarray) – the intensity of the focus field
- (u,ex,ey,ez) (list(ndarray)) – the intensity of the focus field and the complex field components (if return_all_fields is True)
Example
>>> u = focus_field_beam((128,128,128), (0.1,0.1,.1), lam=.5, NA = .4)
References
[1] Matthew R. Foreman, Peter Toeroek, Computational methods in vectorial imaging, Journal of Modern Optics, 2011, 58, 5-6, 339
4.2. Cylindrical Light sheet¶

-
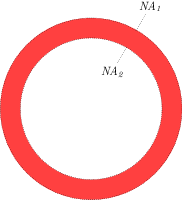
biobeam.focus_field_cylindrical(shape=(128, 128, 128), units=(0.1, 0.1, 0.1), lam=0.5, NA=0.3, n0=1.0, return_all_fields=False, n_integration_steps=100)¶ calculates the focus field for a perfect, aberration free cylindrical lens after x polarized illumination via the vectorial debye diffraction integral (see [2]). The pupil function is given by the numerical aperture NA
Parameters: - shape (Nx,Ny,Nz) – the shape of the geometry
- units (dx,dy,dz) – the pixel sizes in microns
- lam (float) – the wavelength of light used in microns
- NA (float) – the numerical aperture of the lens
- n0 (float) – the refractive index of the medium
- return_all_fields (boolean) – if True, returns u,ex,ey,ez where ex/ey/ez are the complex field components
- n_integration_steps (int) – number of integration steps to perform
- return_all_fields – if True returns also the complex vectorial field components
Returns: - u (ndarray) – the intensity of the focus field
- (u,ex,ey,ez) (list(ndarray)) – the intensity of the focus field and the complex field components (if return_all_fields is True)
Example
>>> u, ex, ey, ez = focus_field_cylindrical((128,128,128), (0.1,0.1,.1), lam=.5, NA = .4, return_all_field=True)
References
[2] Colin J. R. Sheppard: Cylindrical lenses—focusing and imaging: a review, Appl. Opt. 52, 538-545 (2013)
4.3. Bessel Lattices¶
-
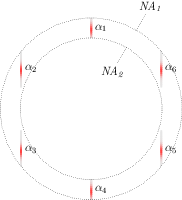
biobeam.focus_field_lattice(shape=(128, 128, 128), units=(0.1, 0.1, 0.1), lam=0.5, NA1=0.4, NA2=0.5, sigma=0.1, kpoints=6, return_all_fields=False, n0=1.0, n_integration_steps=100)¶ Calculates the focus field for a bessel lattice. The pupil function consists out of discrete points (kpoints) superimposed on an annulus (NA1<NA2) which are smeared out by a 1d gaussian of given sigma creating an array of bessel beams in the focal plane (see [3] ).
Parameters: - shape (Nx,Ny,Nz) – the shape of the geometry
- units (dx,dy,dz) – the pixel sizes in microns
- lam (float) – the wavelength of light used in microns
- NA1 (float/list) – the numerical aperture of the inner ring
- NA2 (float/list) – the numerical aperture of the outer ring
- sigma (float) – the standard deviation of the gaussian smear function applied to each point on the aperture (the bigger sigma, the tighter the sheet in y)
- kpoints (int/ (2,N) array) – defines the set of points on the aperture that create the lattice, can be
- a (2,N) ndarray, such that kpoints[:,i] are the coordinates of the ith point
- a single int, defining points on a regular polygon (e.g. 4 for a square lattice, 6 for a hex lattice)
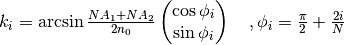
- n0 (float) – the refractive index of the medium
- n_integration_steps (int) – number of integration steps to perform
- return_all_fields (boolean) – if True, returns u,ex,ey,ez where ex/ey/ez are the complex vector field components
Returns: - u (ndarray) – the intensity of the focus field
- (u,ex,ey,ez) (list(ndarray)) – the intensity of the focus field and the complex field components (if return_all_fields is True)
Example
>>> u = focus_field_lattice((128,128,128), (0.1,0.1,.1), lam=.5, NA1 = .44, NA2 = .55, kpoints = 6)
References
[3] Chen et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, (2014).

